Hierarchical Multi-Instance Learning for Transactional Data

Data collection and preparation are critical steps for the success of a machine learning pipeline. Traditionally, manual feature engineering is involved to turn data from ones that humans can interpret to the ones that a machine learning algorithm can understand. Neural networks, as a prime example of machine learning (ML) approaches, are centered around the use of linear algebra and calculus, and as such they require that the data take up numerical form, typically of tensors of fixed size. 

Real-world data are typically complex, as are the objects they describe. Identifying the (finite) set of features that describe all relevant properties of an object can thus be a daunting task that requires expert-level knowledge of the domain. Even then, the resulting representation can still be lossy, and may omit features that are important for the machine learning task at hand. 

As an example, consider a web page. Web pages come in various shapes and provide different types of content. Identifying a list of features that suit all of them and describe all information needed for the ML task is hardly possible: Different pages provide different content, and as such may require different features to describe them. One will also likely need considerably more features to capture all potentially relevant information on a news outlet page compared to a web presentation of a small company. 

We can however leverage the fact that web pages are typically well structured (as is their underlying HTML source code). The pages consist of, e.g., main content with titles and subtitles, menus and their submenus, or header and footer of the page. These components form a hierarchy which is similar across most of the pages, but varies in its complexity (e.g., number of titles or number of items in a menu).  

The variety of data that can be described using similar hierarchies is vast. Examples include, e.g., molecular structures or behavioral logs for malware detection. In this article we focus on identifying fraudulent behavior in financial transaction logs.  

Hierarchical multi-instance learning (or HMIL) [*, **, ***] is a machine learning model and tooling that is designed to deal with such complex types of data without the need to identify the feature set manually. Instead, all features present in the input are preserved and used. This, in combination with the Auto-ML functionality of HMIL libraries (†, ‡​), allows for fast prototyping due to the absence of the feature-engineering step. 

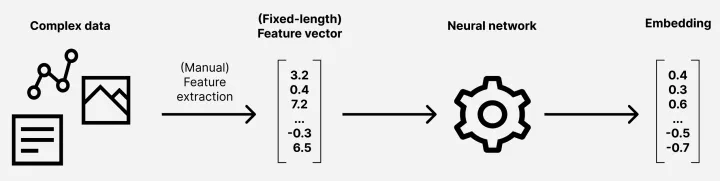
HMIL in a nutshell 

Traditional neural network models consider a single input feature vector and apply a sequence of transformations to calculate the embedding (i.e., numerical representation) for the given input (see Fig. 1). In contrast, HMIL models treat each leaf in the input hierarchy as separate inputs of the model and use recursion (the model itself is a hierarchy!) to calculate embedding of each subtree (see Fig. 2). This means that the embedding zmerchant  captures all relevant information about the merchant in the first transaction (which characterizes both the name of the merchant, as well as the state it operates in). This vector is then propagated upwards in the hierarchy, and it is integrated within ztransaction – a vector which already summarizes all information about the first transaction (i.e., including information about the merchant). 

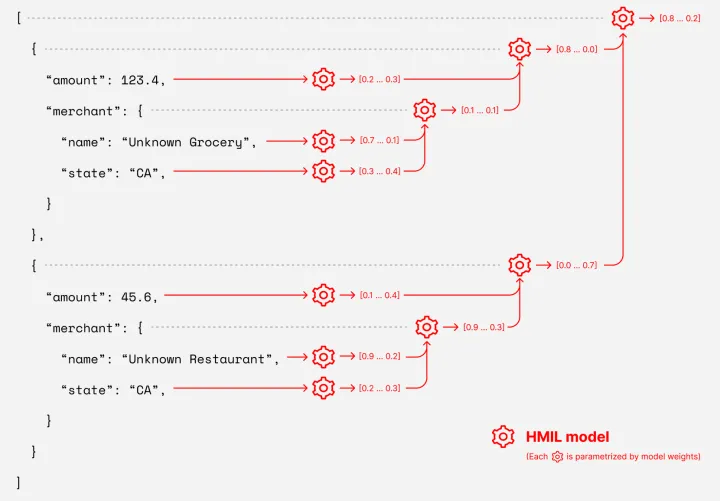
Observe that the number of transactions we are aware of is variable, and in fact, will be growing as we learn about more transactions of the given user. Handling the variable number of child elements is the key challenge when calculating the embeddings (i.e., numerical representations) of a subtree. The reference implementation of HMIL (Mill.jl ​[†]​) handles this by calculating the embedding of each child and aggregating these embeddings using position-invariant aggregation functions, such as maximum, average or count. 

While these simple position-invariant aggregation functions lead to substantial gains in computational efficiency, their use is not suitable for all domains. This is especially true when handling sequential data where the ordering between individual events can be critical for proper interpretation of the data (e.g., an order must precede the payment).  

Towards processing sequential data using HMIL 

To overcome this limitation, we propose to replace the aggregation functions by recurrent cells. Specifically, we use gated recurrent units (GRU) ​[§]​ for this purpose. Instead of calculating, e.g., a simple average of all events in the sequence, the events are fed to the GRU cell in the order they appear in the input. This means that each event is interpreted in the context of all events that precede it. This allows us to distinguish, e.g., between the situations when a user made a payment as a result of an order, and when the payment has been made without a previous order (which may indicate a fraudulent behavior). 

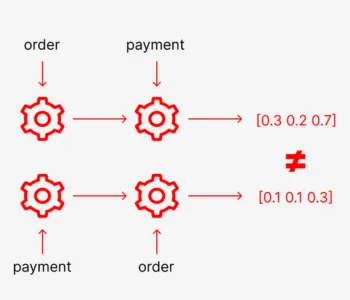
By replacing the aggregation function in the HMIL model by a gated recurrent unit, we allow the model to understand the interplay between sequential events while still retaining its automatic feature extraction capabilities that allow us to handle complex data without extensive feature engineering. Furthermore, we are still able to learn the parametrization of the embedding functions for individual subtrees, including the parameters of the recurrent cells. 

Proof of concept: Fraud detection 

To verify the feasibility and performance of our proposed solution, we have applied HMIL to a synthetic fraud detection dataset [||, ¶]. This dataset has been formed by simulating the behavior of 2,000 users over the timespan of 30 years which resulted in 24.4 million transactions of which 0.12% are fraudulent. The dataset is generated in a way to reflect statistical properties of the US-based population including, e.g., the travel patterns of individual users. 

Most of the previous ML approaches for handling this dataset rely on classifying each transaction in the dataset separately. In contrast, our HMIL-based approach handles a window of 20 transactions of a given user at once and aims at classifying whether the last transaction within the window is fraudulent or not. This setting corresponds to a real-world scenario where the transactions of a user are processed in a streaming way: We are asked to classify whether the current transaction is fraudulent, but we are allowed to consult previous behavior of the user to make the decision. 

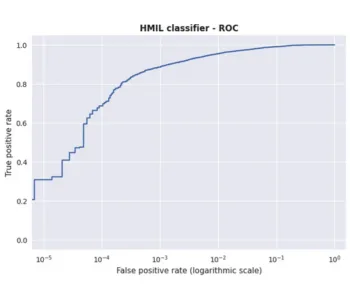
Even without any fine-tuning of the training procedure of the HMIL model (using most of the out-of-the-box Auto-ML functionality of HMIL libraries), we have been able to achieve F1 scores of over 0.95 on the testing split. In comparison, the state-of-the-art TabBERT approach [#] which also addresses the sequential nature of the data achieves F1 score of 0.86 only (we report numbers as presented in the original publication)."

While both TabBERT and our approach use a similar approach to handle the sequentiality by considering windows of adjacent transactions and feeding them to a recurrent neural network, the key difference lies in the way the embeddings of individual transactions are obtained. Unlike our HMIL approach, TabBERT relies on a language model to embed the data which is trained independently of the fraud detection task. This is in contrast with our HMIL approach which trains the fraud classifier and the HMIL-based embedder at the same time. 

The difference in performance highlights the benefits of using HMIL architecture for processing complex data which we have also seen in other applications. The automatic feature extraction capabilities of HMIL allowed us to obtain strong performance with minimum optimization of the training process.